Martin Schwarzbauer, at PCO, and Bernd Jähne, at HCI, Heidelberg University, discuss the need for quasi lossless image data compression from 16-bit images to 8-bit or less
For state-of-the-art CMOS image sensors a digital resolution of 8-bit is no longer sufficient and, especially for scientific CMOS (sCMOS) image sensors, nearly 16-bit is necessary. The reason for the larger dynamic range is, on the one hand, the very low standard deviation of the dark noise, with just about 1 electron, while, on the other hand, the full-well capacity is in the order of 30,000 electrons or higher. In the near future image sensors will be available with the same low dark noise but an even higher full-well capacity, so the quantisation of 16-bit would no longer be sufficient. Higher resolution requires more storage space, the need for faster data interfaces caused by higher bandwidth, and image processing algorithms may require more processing time, which has an impact on real-time processing applications.
The compression algorithm
Image sensors with such a low dark noise are dominated by photon noise. Therefore, the variance of the noise is about equal to the mean number of accumulated charge units. The standard deviation of the noise consequently increases with the square root of the mean digital value. Any equidistant quantisation is a clear mismatch in this situation. The quantisation must be fine enough to resolve the small random fluctuations at low signal levels, but it is much too fine at high signal levels.
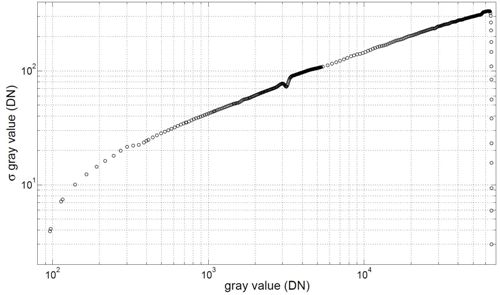
Figure 1: Standard deviation (σg) of the temporal noise for the PCO Edge 5.5 sCMOS camera measured in fast-scan mode.
As an illustration, the standard deviation of the noise of a PCO Edge 5.5 sCMOS camera is shown in Figure 1. It covers more than two orders of magnitude. It is about four for the dark image, but more than 300 close to saturation. Thus, the quantisation is more than two orders of magnitude too fine in the bright parts of the image, and more than 8 bits just carries the photon noise of the data.
The questions arise whether it is possible to apply a nonlinear transformation in such a way that the temporal noise is independent of the grey value, and what is the minimum number of bits with which a signal can be presented without any significant loss of information? It would be especially useful if an 8-bit quantisation could be achieved for up to 16-bit image data.
To find a solution for these questions, firstly the nature of the photon noise and the theoretical linear camera model (see EMVA 1288 Working Group) has to be considered, and secondly the influence of additional noise caused by quantisation has to be taken into account. A detailed derivation of the solution is too long for this article, but it can be found in the paper referenced at the end of the page.
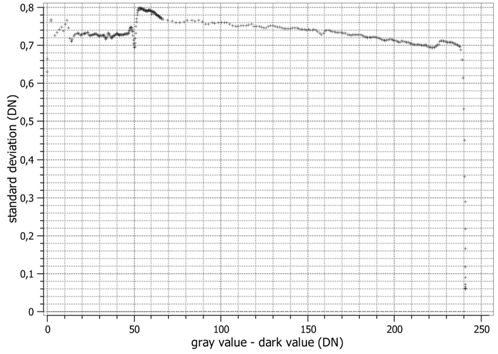
Figure 2: Measured temporal noise in the compressed signal.
In one example the nonlinear transformation scheme was applied to the PCO Edge 5.5 operated in fast-scan mode, and an almost constant, signal-independent noise is achieved (Figure 2) as predicted by the theoretical considerations. The original image is quantised with 16-bit. Using procedures detailed in the EMVA 1288 standard, the standard deviation of the dark noise and the system gain were measured (upper row in Table 1). The compression parameters are set in a way that only 8-bit per pixel is required instead of 16-bit, resulting in a compression ratio of two. After measuring the parameters according to EMVA 1288 with the decompressed data (middle row in Table 1), there is additional noise that results in higher system gain. After correction of the system gain (lower row in Table 1) the measurement results fit very well with the original measurement without compression.
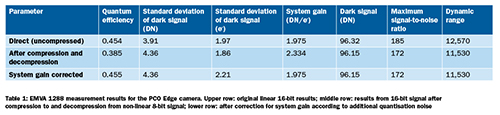
Table 1: EMVA 1288 measurement results for the PCO Edge camera. Upper row: original linear 16-bit results; middle row: results from 16-bit signal after compression to and decompression from non-linear 8-bit signal; lower row: after correction for system gain according to additional quantisation noise.
The interest in compression was because the Camera Link interface found on the PCO Edge camera had limited bandwidth – this was the fastest interface at that time – and the requirement to stream the data at a higher rate. An approach of a simple nonlinear transformation was used by PCO, but a convincing solution was only found through the cooperation between the Heidelberg Collaboratory for Image Processing (HCI) and PCO. Both parties benefit from each other; PCO gets access to wide-ranging interdisciplinary knowledge of HCI, and HCI gets access to high-end camera equipment for applied research.
Reference
B. Jähne and M. Schwarzbauer: Noise equalisation and quasi lossless image data compression – or how many bits needs an image sensor? Technisches Messen, 83, 16-24, 2016. http://dx.doi.org/10.1515/teme-2015-0093

